In hyperbolic geometry distances are not measured in the usual way. In the hyperbolic metric the shortest distance between two points is no longer along a straight line, but along a different kind of curve.

2 Dimensions

In hyperbolic geometry, because distances are measured differently, the points that are equally far away from our point c still form a circle, but c is no longer at what looks like its centre. The circumference of this hyperbolic circle is proportional not to its radius, but to \(e^{radius}\), where e is the base of the natural logarithm and is roughly equal to 2.718. If the radius is large, then this means that the circumference of a hyperbolic circle is much larger than that of a Euclidean circle. So to fit into ordinary Euclidean space, a big hyperbolic disc has to crinkle up round its edges like a kale leaf. Once you start looking for it, you see this type of growth throughout the natural world.

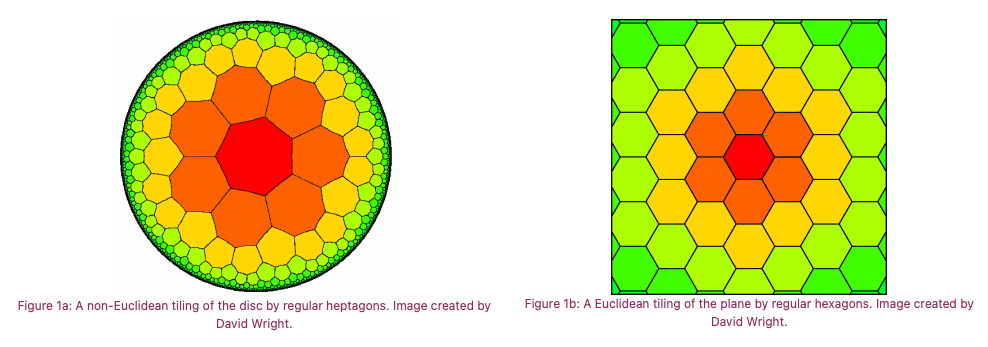
Despite appearances, in the world of hyperbolic geometry the tiles in the above figure all have the same size and shape. To fit the tiles into a Euclidean picture, we have to shrink their apparent size as we move away from the centre of the disc, so that to our Euclidean glasses the tiles look smaller and smaller as they pile up near the edge of the disc. Since you can fit infinitely many layers of tiles between the centre of the disc and its boundary, in our hyperbolic way of measuring, the boundary must be infinitely far away from the centre. In this strange geometry the diameter of the disc is infinite. For this reason, the boundary circle is called the circle at infinity.

3 Dimensions

Now imagine a similar geometry in three dimensions. Just as the two-dimensional hyperbolic plane can be visualised as a disc enclosed by its circle at infinity, so the three-dimensional hyperbolic universe can be visualised as a solid ball, enclosed in a Euclidean sphere. The sphere’s boundary is infinitely far, in hyperbolic terms, away from its centre.

Math

To create a two-dimensional tiling, whether it’s Euclidean, or hyperbolic, you need a way of creating identical copies of an initial tile and placing them alongside each other. Mathematically, this job is done by reflections, rotations and translations: you get to each tile either by shifting your initial tile into a given direction by a given distance — this is known as a translation — by reflecting it in an axis, or by rotating it through a given angle around a fixed point. Or, indeed, by a combination of any of these three movements.

But how can we describe these movements? Remember that our symmetries leave hyperbolic distance intact. But we are working on the bounding sphere at infinity, where we can no longer measure distance in the same way. In fact, on the window pane at infinity it is impossible to find a way of measuring distance that is preserved. But all is not lost: it turns out that the transformations we are looking for do leave something intact. They transform circles into circles, with changes of radius being allowed. Such transformations are called Mobius Transformations, after the German mathematician August Möbius.