Relationships between image pixels
Tags :: Image processing
A pixel \(p\) at \((x, y)\) has four horizontal and vertical neighbors \(N_4(p)\) or 4 neighbors in blue.
Four diagonal neighbors of \(p\) or \(N_D(p)\) in green.
\(N_8(p) = N_4(p) \cup N_D(p)\) or 8 neighbors.

Adjacency
V is the gray levels of similarity
Where \(V = \{\text{gray levels of similarity\}}\)
Two pixels \(p\) and \(q\) have a pixel value from \(V\):
\[ f(p) \in V \text{ and } f(q) \in V \]
- 4-adjacency if \(q \in N_4(p)\)
- 8-adjacency if \(q \in N_8(P)\)
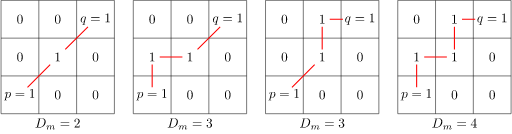
- m-adjacency if
- \(q \in N_4(p)\) or
- \(q \in N_D(p) \text{ and } N_4(p) \cap N_4(p)\) has no pixels whose values are from \(V\)
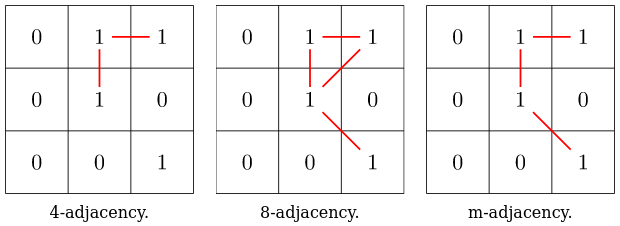
m-adjacency will be a single path between values.
Connectivity
Have \(p\) at \((x_0, y_0) = (x, y)\) and \(q\) at \((x_n, y_n) = (s,t)\)
A sequence of distinct pixels \((x_0,y_0),(x_1,y_1),\cdots,(x_n,y_n)\) is a path from \(p \to q\) is \((x_i, y_i)\) and \((x_{i-1}, y_{i-1})\) are adjacent for \(1\leq i\leq n\).
4, 8, or m-path can be used depending on adjacency.
Let \(S\) be a subset of pixels in an image, two pixels \(p\) and \(q\) are connected in \(S\) if there exists a path in \(S\) between the two pixels.
Connected component
For \(p \in S\), the set of pixels connected to it in \(S\) is a connected component of \(S\).
Connected set
If \(S\) has only one connected component it is called a connected set.
Adjacent subsets
Two subsets \(S_1\) and \(S_2\) are adjacent if a pixel in \(S_1\) is adjacent to another pixel in \(S_2\).
Region and boundary
Let \(R\) be a subset of pixels in an image, \(R\) is a region of the image if \(R\) is a connected set.
The boundary (border or contour) of a region \(R\) is the set of pixels in the region that have neighbors that are not in \(R\).
If \(R\) is an entire image, then the first and last rows and columns are used as the boundary.
Distance measures
Distance requirements
\(p\) at (\(x, y\)), \(q\) at \((s, t)\) and \(z\) at \((v,w)\).
\(D\) is a distance function or metric if
- \(D(p,q)=0\text{ iff }p=q\),
- \(D(p,q)=D(q,p)\), and
- \(D(p,z)\leq D(p,q)+D(q,z)\)
Euclidean
\[ D_e(p,q)=\left[(x-s)^2+(y-t)^2\right]^{1/2} \]
Manhattan
\[ D_4(p,q)=|x-s|+|y-t| \]
Chessboard
\[ D_8(p,q)=\max\left(|x-s|,|y-t|\right) \]
Dm distance
Based on m-adjacency: Shortest path