Digital Image Processing
Tags :: Image processing
What is an image?
Mathematically, images are a two-dimensional function of \(f(x,y)\), where \(x\) and \(y\) are spatial coordinates, and \(f\) is the gray level of the image at \((x,y)\). In this, \(x\), \(y\), and \(f\) are finite and discrete. Operating as a discrete function, \(f\) will appear as a stepping function with no gradient between values.
\[ f(x,y) \to (r,g,b) \to \begin{cases} r \text{ or }\\ g \text{ or }\\ b \end{cases} \]
Optionally, \(t\) (time) can be added for image sequences. A 2D image is represented as a finite set of digital values.
Digital imaging systems operate through approximation, and the light intensity of each cell will only be as accurate as the level of approximation.
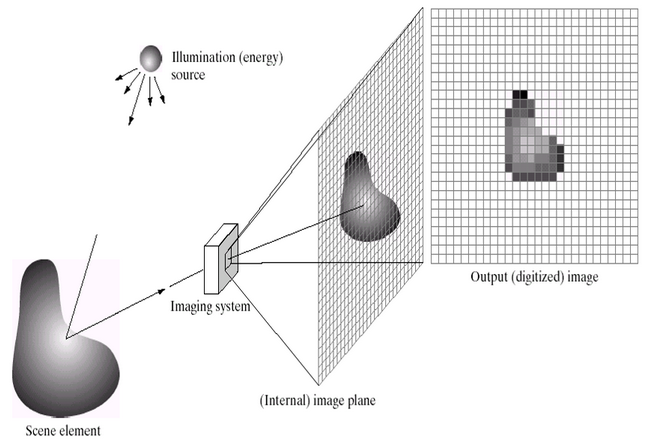
Processing
Digital image processing focuses on two main tasks:
- Improvement of pictorial information for human interaction.
- Processing of image data for storage, transmission, and representation for machine perception.
Computerized processes can be split into three levels:
- Low-level:
- Noise reduction
- Contrast enhancement
- Image sharpening
- Mid-level:
- Edges
- Contours
- Identity
- High-level:
- Making sense of recognized objects
Image processing typically falls within low and mid-level processes, while image analysis or computer vision falls under high-level processing.
Waves
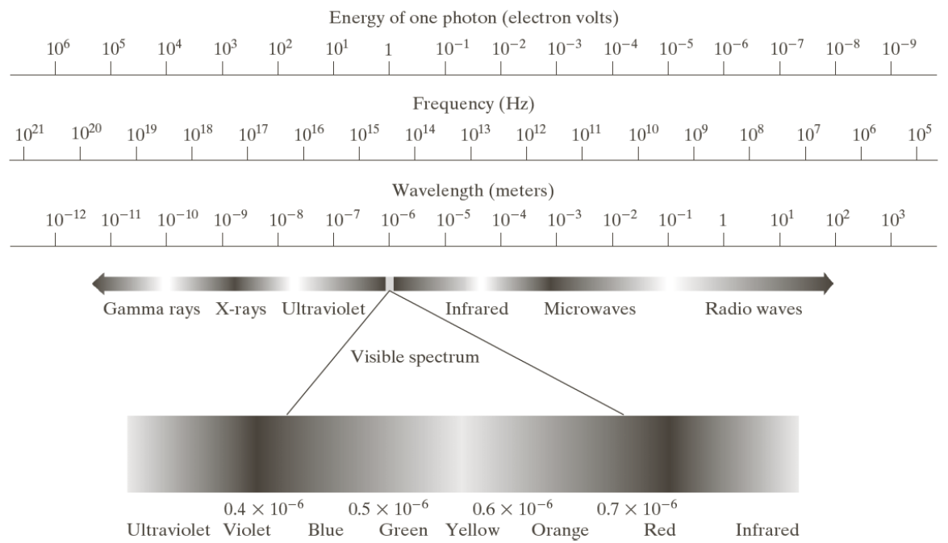
- Frequency: The number of cycles per second.
- Wavelength: \(\lambda = \frac{c}{\nu}\)
Where:
- \(c\): Speed of light (2.998 x 10^8 m/s)
- \(\nu\): Frequency in Hz
- 1 Hz is 1 cycle of a sinusoidal wave per second
- Units of wavelength: m, microns (\(\mu m\), \(10^{-6}\) m)
Energy: \(E = h \nu\)
Where:
- \(h\): Planck’s constant (\(4.135,667,66×10^{-15}\) eV)
- Units of energy: electron-volt (eV)
Frequency and energy are proportionally related: the higher the frequency, the higher the energy.
Digital Image cont.
\[ f(x,y) = i(x,y) \times r(x,y) \]
Where:
- \(i(x,y) \in [0,\infty)\): Illumination, characteristics of the energy source.
- \(r(x,y) \in [0,1]\): Reflectance, characteristics of the object sensed.
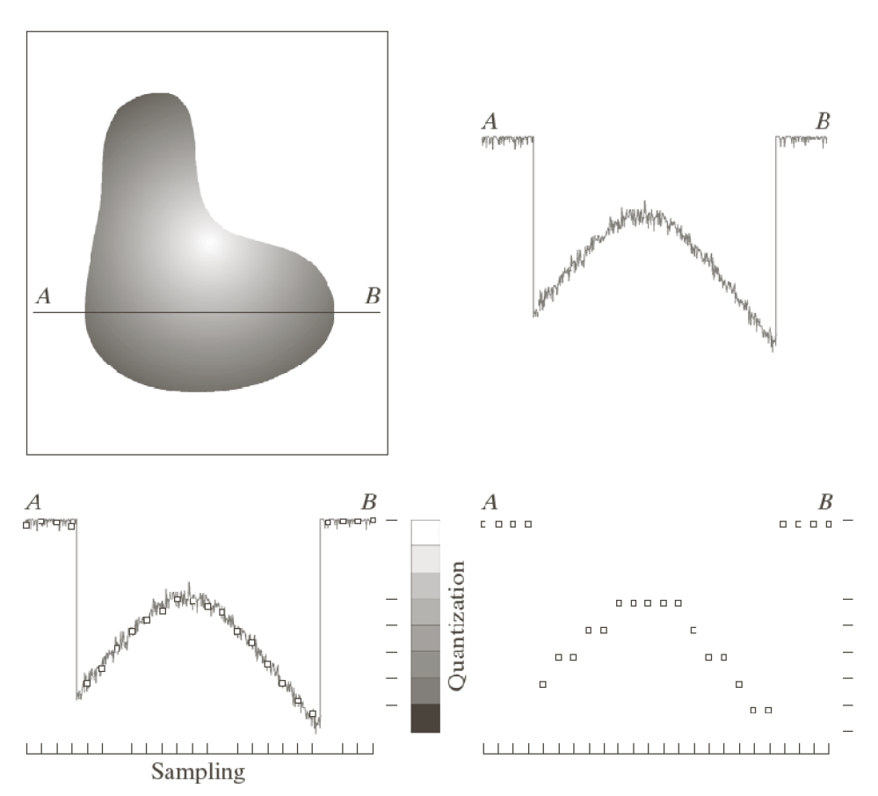
Quantization
Quantization involves taking a linear sample of an image and converting it to grayscale.
Representation
An image is represented by \(M\) rows and \(N\) columns, forming an \(M \times N\) matrix:
\[ f(x,y) = \begin{bmatrix} f(0,0) & \cdots & f(0,N-1) \\ \vdots & \ddots & \vdots \\ f(M-1,0) & \cdots & f(M-1,N-1) \end{bmatrix} \mathbf{A} = \begin{bmatrix} a_{0,0} & \cdots & a_{0,N-1} \\ \vdots & \ddots & \vdots \\ a_{M-1,0} & \cdots & a_{M-1,N-1} \end{bmatrix} \]
Bits
MSB LSB
┌───┬───┬───┬───┬───┬───┬───┬───┐
│ 1 │ 0 │ 0 │ 1 │ 0 │ 1 │ 0 │ 1 │
└───┴───┴───┴───┴───┴───┴───┴───┘
╰───────────── 1 byte ──────────╯
- LSB: Least significant bit.
- MSB: Most significant bit.
The LSB has the least impact on the byte’s value, while the MSB has the most.
1 byte = 8 bits.
Unsigned integer \(\in [2^0, 2^8 - 1] = [0, 255]\).
Grey levels
- Number of bits per pixel: \(k\).
- Grey levels: \(L = 2^k\).
- To find \(k\): \(k = \frac{\log(L)}{\log(2)}\).
\[ f(x,y) = \begin{cases} 0 & \text{black} \\ L-1 & \text{white} \end{cases} \]
Storage bits and bytes
- Storage bits: \(b = M \times N \times k\).
- Storage bytes: \(B = \left\lceil \frac{b}{8} \right\rceil\).