A mobius transformation of the complex plane is a rational function of the form \[ f(z) = \frac{az + b}{cz + d} \] of one complex variable \(z\). The coefficients a, b, c, d are complex numbers satisfying \(ad - bc \neq 0\).

Fixed point theorem

Any mobius transformation \(T : \mathbb{C}^+ \rightarrow \mathbb{C}^+\) fixes 1, 2 or all points of \(\mathbb{C}^+\).

Fundemental theorem

With the fixed point theorem, the fundamental theorem of mobius transformations can be proved.

The theorem states that if we want to induce a one-to-one and onto motion of the entire extended plane that sends three points \((z_1, z_2, z_3)\) to another set of points \((w_1, w_2, w_3)\), then there is a mobius transformation that will do the trick, and there is only one.

The image below shows \(z_1 \rightarrow w_1\), \(z_2 \rightarrow w_2\), \(z_3 \rightarrow w_3\)

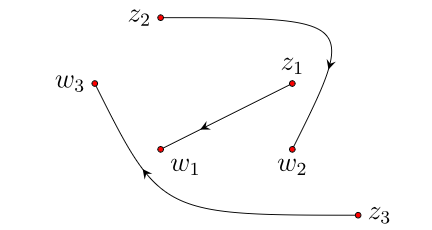
Theorem: There is a unique mobius transformation taking any three distinct points of \(C^+\) to any three distinct points of \(C^+\).

We now apply the linear transformation \(z \rightarrow z - z_1 z_2 - z_1\) which transforms the unique points \([z_1,z_2,z_3]\) to the points \([0, 1, w=z_3 - z_1 z_2 - z_1\) .